CIRCUITOS ELECTRICOS

1. CIRCUITOS ELÉCTRICOS

1.1 DEFINICIÓN

Es una interconexión de elementos eléctricos unidos entre sí de forma que pueda fluir una corriente eléctrica.

Por parte de la ELECTRÓNICA

      Se define a los  circuito  a un conjunto de conductores que recorre una corriente eléctrica, y en el cual generalmente hay intercalados aparatos productores o consumidores de dicha corriente.

Por parte de la  LÓGICA

         Se habla de circuitos de conmutación, que están compuestos por una serie de contactos que representan las variables lógicas de entrada y una o varias cargas que representan las variables lógicas o funciones de salida. Los contactos pueden ser normalmente abiertos (NA) o normalmente cerrados (NC).

Por lo tanto la Lógica Matemática interviene de cierto modo en la construcción de circuitos, debido a los enlaces de verdad y falsedad que se dan a la hora de poner en práctica la construcción de un circuito abierto o cerrado.

1.2  CORRIENTE ELÉCTRICA

La corriente o intensidad eléctrica es el flujo de carga por unidad de tiempo que recorre un material. Se debe al movimiento de los  electrones en el interior del material.

        1.2.1     CORRIENTE CONTINUA

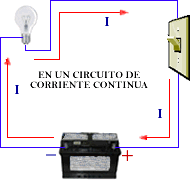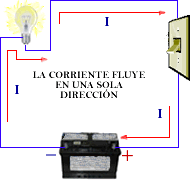
Es aquella corriente en donde los electrones circulan en la misma cantidad y sentido, es decir, que fluye en una misma dirección. Su polaridad es invariable y hace que fluya una corriente de amplitud relativamente constante a través de una carga. A este tipo de corriente se le conoce como corriente continua (cc) o corriente directa (cd), y es generada por una pila o batería.

                                                        Figura 1: Corriente Continua

      

                       1.2.1.1 PILAS Y BATERÍAS

 Las pilas y las baterías son un tipo de generadores que se utilizan como fuentes de electricidad.

                                                               Figura 2:  Pilas y Baterias

Las baterías, por medio de una reacción química producen, en su terminal negativo, una gran cantidad de electrones (que tienen carga negativa) y en su terminal positivo se produce una gran ausencia de electrones (lo que causa que este terminal sea de carga positiva).

 1.2.2     CORRIENTE ALTERNA

La corriente alterna es aquella que circula durante un tiempo en un sentido y después en sentido opuesto, volviéndose a repetir el mismo proceso en forma constante. Su polaridad se invierte periódicamente, haciendo que la corriente fluya alternativamente en una dirección y luego en la otra. Se conoce en castellano por la abreviación CA y en inglés por la de AC.

Este tipo de corriente es la que nos llega a nuestras casas y sin ella no podríamos utilizar nuestros artefactos eléctricos y no tendríamos iluminación en nuestros hogares. Este tipo de corriente puede ser generada por un alternador o dinamo, la cual convierten energía mecánica en eléctrica. 

                                                           Figura 3: Corriente Alterna

1.3 CIRCUITOS ABIERTOS Y CERRADOS

       1.3.1     CIRCUITO ABIERTO

Es cuando la Trayectoria de la corriente tiene alguna interrupción, hay una diferencia de potencial pero no hay corriente. 

                                                       Figura 4: Circuito Abierto

 

       1.3.2     CIRCUITO CERRADO

Es cuando la Trayectoria de la corriente no tiene ninguna  interrupción, hay diferencia de potencial y corriente.

                                                          Figura 5: Circuito Cerrado

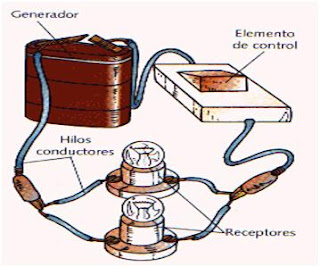
1.4 PARTES DE UN CIRCUITO ELÉCTRICO

 

Figura 6: Componentes Eléctricos

      1.4.1     SIMBOLOGÍA

                                                    Figura 7: Símbolos Eléctricos 

1.5  CIRCUITOS EN SERIE Y PARALELO

        1.5.1     CIRCUITO EN SERIE

Se define un circuito serie como aquel circuito en el que la corriente eléctrica solo tiene un solo camino para llegar al punto de partida, sin importar los elementos intermedios. En el caso concreto de solo arreglos de resistencias la corriente eléctrica es la misma en todos los puntos del circuito.

                                                   Figura 8: Circuito en Serie 

        1.5.2     CIRCUITO EN PARALELO

Se define un circuito paralelo  como aquel circuito en el que la corriente eléctrica se  bifurca en cada nodo. Su característica más importante es el hecho de que el potencial en cada elemento del circuito tiene la misma diferencia de potencial.

                                                        Figura 8: Circuito en Paralelo

        1.6 EJEMPLO DE CIRCUITOS EN SERIE Y PARALELO

___________________________________________________________

Frase Celebre

"Cuando las leyes de la matemática se refieren a la realidad, no son ciertas; cuando son ciertas, no se refieren a la realidad." Albert Einstein (1879-1955) 

 _________________________________________________________________________________

CONECTORES LOGICOS

LÓGICA MATEMÁTICA

La lógica matemática es una parte de la lógica y las matemáticas, que consiste en el estudio matemático de la lógica y en la aplicación de este estudio a otras áreas de las matemáticas. La lógica matemática tiene estrechas conexiones con la ciencias de la computación y la lógica filosófica.

La lógica matemática estudia los sistemas formales en relación con el modo en el que codifican nociones intuitivas de objetos matemáticos como conjuntos, números, demostraciones y computación.

La Negación

La operación unitaria de negación, no es cierto que se representa por “¬” y tiene la siguiente tabla de verdad de verdad

p	¬p
V	F
F	V

La conjunción de las proposiciones p, q es la operación binaria que tiene por resultado p y q, se representa por p^q, y su tabla de verdad es:

p

q

p^q

V	V	V
V	F	F
F	V	F
F	F	F

La disyunción de dos proposiciones p, q es la operación binaria que da por resultado p ó q, notación p v q, y tiene la siguiente tabla:

p	q	p v q
V	V	V
V	F	V
F	V	V
F	F	F

La o excluyente, que algunos también le llaman o exclusiva, y que indica que una de las dos proposiciones se cumple, pero no las dos. Este caso corresponde por ejemplo a: Hoy compraré un libro o iré al cine; se sobrentiende que una de las dos debe ser verdadera, pero no la dos. Se representa por p XOR q y su tabla de verdad es:

p	q	p XOR q
V	V	F
V	F	V
F	V	V
F	F	F

Por último, también es muy común utilizar una disyunción como la siguiente: El menú incluye café o té. En este caso se esta dando una disyuntiva diferente pues no se pueden las dos simultáneamente como en el caso anterior, pero aquí si es válido el caso donde las dos son falsas. Es el caso “no ámbas”, se puede representar por p § q y su tablas es

p	q	p § q
V	V	F
V	F	V
F	V	V
F	F	V

La condicional de dos proposiciones p, q da lugar a la proposición; si p entonces q, se representa por p → q, y su tabla de verdad está dada por:

p	q	p→q
V	V	V
V	F	F
F	V	V
F	F	V

La bicondicional de dos proposiciones p, q da lugar a la proposición; p si y sólo si q, se representa por p ↔ q su tabla de verdad está dada por:

p	q	p ↔ q
V	V	V
V	F	F
F	V	F
F	F	V

Contrucción de Tablas de Verdad

Como ya sabemos la sintaxis en lógica es la forma correcta de escribir una fórmula y la semántica es lo que significa. Como en lógica solamente tenemos dos valores una fórmula solamente puede ser verdadera o falsa. Para determinar su valor seguimos las reglas simples que dimos en las definiciones básicas de acuerdo a su tabla de verdad. Esto lo hacemos mediante interpretaciones. Una interpretación de una fórmula es un conjunto de valores que se les asignan a sus proposiciones atómicas.

Al interpretar una fórmula lo que finalmente vamos a obtener es un valor de verdad, bien sea verdadero o falso. Pero para poder encontrarlo muchas veces el proceso en laborioso porque puede estar formada por varias proposiciones atómicas. Primeramente se le asignan valores de verdad a los átomos y se puede encontrar el valor de la expresión.

Si deseamos hacerlo en general, debemos analizar todas las posibilidades, esto se puede hacer construyendo una tabla de verdad. Para fines prácticos cuando se tienen varios átomos las tablas de verdad no resultan prácticas por lo que analizaremos solamente expresiones con tres átomos como máximo.

Por supuesto que se puede construir una tabla para un número mayor de átomos, pero notemos que por cada átomo que se aumente el número de renglones se duplica. Esto es, para un átomos son dos renglones, para dos átomos son cuatro, para tres átomos son ocho, para cuatro dieciséis, etc.

Algoritmo para construir una tabla de verdad de una fórmula en lógica de proposiciones.

1. Escribir la fórmula con un número arriba de cada operador que indique su jerarquía. Se escriben los enteros positivos en orden, donde el número 1 corresponde al operador de mayor jerarquía. Cuando dos operadores tengan la misma jerarquía, se le asigna el número menor al de la izquierda.

2. Construir el árbol sintáctico empezando con la fórmula en la raíz y utilizando en cada caso el operador de menor jerarquía. O sea, del número mayor al menor.

3. Numerar las ramas del árbol en forma secuencial empezando por las hojas hacia la raíz, con la única condición de que una rama se puede numerar hasta que estén numerados los hijos. Para empezar con la numeración de las hojas es buena idea hacerlo en orden alfabético, así todos obtienen los renglones de la tabla en el mismo orden para poder comparar resultados.

4. Escribir los encabezados de la tabla las fórmulas siguiendo la numeración que se le dió a las ramas en el árbol sintáctico.

5. Asignarle a los átomos, las hojas del árbol, todos los posibles valores de verdad de acuerdo al orden establecido. Por supuesto que el orden es arbitrario, pero como el número de permutaciones es n!, conviene establecer un orden para poder comparar resultados fácilmente.

6. Asignar valor de verdad a cada una de las columnas restantes de acuerdo al operador indicado en el árbol sintáctico utilizando la tabla de verdad correspondiente del Tema 1.3 Conexiones Logicas y Jerarquias. Conviene aprenderse de memoria las tablas de los operadores, al principio pueden tener un resumen con todas las tablas mientras se memorizan.

7. La última columna, correspondiente a la fórmula original, es la que indica los valores de verdad posibles de la fórmula para cada caso.

EJEMPLO

i) (p → ¬q) v (¬p v r)

1	2	3	4	5	6	7	8
p	q	r	¬ q	¬ p	p → ¬q	¬p v r	(p → ¬q) v (¬p v r)
V	V	V	F	F	F	V	V
V	V	F	F	F	F	F	F
V	F	V	V	F	V	V	V
V	F	F	V	F	V	F	V
F	V	V	F	V	V	V	V
F	V	F	F	V	V	V	V
F	F	V	V	V	V	V	V
F	F	F	V	V	V	V	V

BIBLIOGRAFIA

http://www.mitecnologico.com/Main/TablasDeVerdad

http://es.wikipedia.org/wiki/Tabla_de_verdad

________________________________________________________________________

Frase Celebre

"Las Matemáticas pueden ser definidas como aquel tema en el cual ni sabemos nunca lo que decimos ni si lo que decimos es verdadero."  Bertrand Russell (1872-1970)  

Estudiando no molestar

 __________________________________________________________________________________________________